Chua's Oscillator
The Chua's oscillator is a simple nonlinear 3rd-order electronic circuit, developed by Leon Chua, showing a rich variety of nonlinear dynamical phenomena, including all of the standard bifurcations and routes to chaos.
Simulation
Circuit
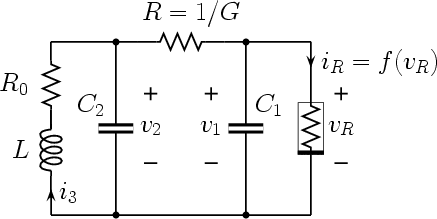
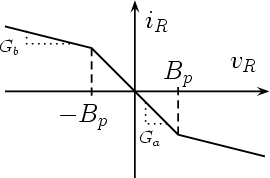
| Figure 1: | Chua’s oscillator and Chua’s diode |
The applet shows a simulation of Chua's oscillator, plotting the
voltage measured across C1 against the voltage measured across
C2. This corresponds to the display on an X-Y
oscilloscope with probes connected across these capacitors. The
initial values of the components used in the applet lead to an equilibrium point and are the values used to build a real circuit
(see here for details).
The different dynamical behaviours - periodic orbits, bifurcations etc.- can be observed
by carefully decreasing R or C1, (e.g. decrease
R in steps of 10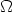
to 1.5 k 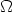). Eventually, the circuit shows strange attractors and
chaotic dynamic, interlaced with periodic windows. The simulation compares well with what is actually seen on an oscilloscope. Chaos seems to develop following
a period-doubling route, but other routes to chaos can be followed, changing the values of the components (see the book edited by R. N. Madan
[3] for an extensive gallery of attractors from Chua's oscillator).
Details on how the circuit works can be found in this Kennedy's paper, whereas the description of how to build the physical circuit can be found in another paper by Kennedy. More details on the design of the Chua's oscillator and the related piece-wise linear resistor (called the Chua's diode) can be found here.
The state equations simulated by the applet have a different form with respect to the one used in the original Chua's paper [2], (see also [3], page xv).
In the applet the state variable are defined as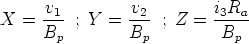
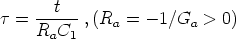
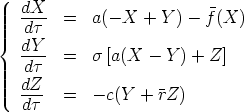
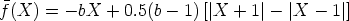
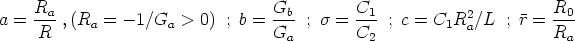
Dynamical behaviours
A few different dynamical behaviours observed for particular values of the bifurcation parameter R are listed in Table I, where the eigenvalues in the inner and outer linear regions are also shown.
| Table I: | A few different dynamical behaviours and the corresponding values of the bifurcation parameter R |
| R (  ) | Dynamical behaviour | Eigenvalues | |
| Inner region | Outer region | ||
| 2000 | equilibrium point | 0.400811 -0.0693060 + j0.281099 -0.0693060 - j0.281099 |
-0.185191 -0.00580252 + j0.247304 -0.00580252 - j0.247304 |
| 1911 | Hopf bifurcation | 0.376557 -0.0741200 + j0.275424 -0.0741200 - j0.275424 |
-0.230693 0.000007 + j0.249053 0.000007 - j0.249053 |
| 1870 | period 1 limit cycle | 0.364676 -0.0765264 + j0.272294 -0.0765264 - j0.272294 |
-0.252123 0.00237552 + j0.250134 0.00237552 - j0.250134 |
| 1850 | period 2 limit cycle | 0.358702 -0.0777453 + j0.270625 -0.0777453 - j0.270625 |
-0.262704 0.00346022 + j0.250707 0.00346022 - j0.250707 |
| 1840 | period 4 limit cycle | 0.355669 -0.0783660 + j0.269752 -0.0783660 - j0.269752 |
-0.268029 0.00398554 + j0.251002 0.00398554 - j0.251002 |
| 1830 | spiral-Chua strange attractor | 0.352604 -0.0789943 + j0.268853 -0.0789943 - j0.268853 |
-0.273378 0.00449965 + j0.251303 0.00449965 - j0.251303 |
| 1828 | period 3 periodic window | 0.351987 -0.0791209 + j0.0791208 -0.0791209 - j0.0791208 |
-0.274451 0.00460114 + j0.251364 0.00460114 - j0.251364 |
| 1820 | spiral-Chua strange attractor | 0.349507 -0.0796301 + j0.267925 -0.0796301 - j0.267925 |
-0.278753 0.00500269 + j0.251610 0.00500269 - j0.251610 |
| 1796 | double-scroll strange attractor | 0.341937 -0.0811869 + j0.265577 -0.0811869 - j0.265577 |
-0.291762 0.00616566 + j0.252364 0.00616566 - j0.252364 |
| 1640 | 4+4 periodic window | 0.287098 -0.0922986 + j0.244676 -0.0922986 - j0.244676 |
-0.381179 0.0123424 + j0.257658 0.0123424 - j0.257658 |
| 1630 | double-scroll strange attractor | 0.283174 -0.0930582 + j0.242884 -0.0930582 - j0.242884 |
-0.387268 0.0126653 + j0.258008 0.0126653 - j0.258008 |
| 1610.5 | 3+3 periodic window | 0.275345 -0.0945477 + j0.239176 -0.0945477 - j0.239176 |
-0.399290 0.0132725 + j0.258692 0.0132725 - j0.258692 |
| 1571 | 2+2 periodic window | 0.258681 -0.0975737 + j0.230666 -0.0975737 - j0.230666 |
-0.424292 0.0144156 + j0.260077 0.0144156 - j0.260077 |
| 1530 | double-scroll strange attractor | 0.240021 -0.100653 + j0.220073 -0.100653 - j0.220073 |
-0.451254 0.0154866 + j0.261509 0.0154866 - j0.261509 |
| 1515 | large limit cycle | 0.232773 -0.101737 + j0.215637 -0.101737 - j0.215637 |
-0.461398 0.0158509 + j0.262029 0.0158509 - j0.262029 |
Last updated: